Finding Roots of a Polynomial

What Does it Mean?

“Finding roots of a polynomial” means finding the set of input values for the polynomial that will result in an output of 0.

This may seem very restrictive, but you have to remember that if you just add or subtract a constant to your polynomial, you can find input values that result in some specific output value (not just 0).

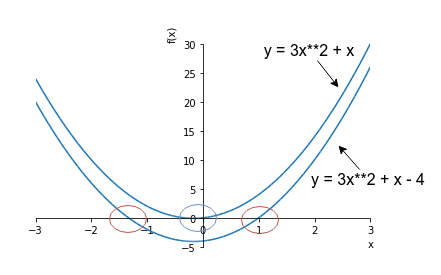
For example, if your polynomial is $y = 3x^2 + x$, you can subtract 4 to make it $y = 3x^2 + x - 4$. You basically moved your function 4 units “down”. If you find input values that makes this lower function 0, that is the same thing as finding input values that makes the higher (original) function 4. So, although finding roots of a polynomial is defined as finding input values that make the output 0, you can think of it a little more generally, think of it as finding the input values that produce a specific output.

This picture should make it a bit clearer:

How to do it

You can do it analytically or numerically (i.e. numerical methods). You can only do it analytically for simple polynomials (quadratics, cubics)but anything with a higher degree becomes extremely difficult to do analytically, thus you must look to numerical methods. We will only discuss numerical methods in this post.

Let’s look at 2 numerical methods for finding the roots of a polynomial.

Newton’s Method

Pick an arbitrary initial input (or set of inputs if you are working with a multivariate polynomial). Find the gradient at your input. If you are currently above 0 and the gradient is negative, move your input a little in the opposite direction of the gradient (i.e. go down hill towards 0). If you are currently above 0 and the gradient is positive, move a little in the opposite direction of the gradient (again, going down hill towards 0). If you are currently below 0, and the gradient is positive, move a little in the direction of the gradient (heading uphill towards 0). You get the point. We can express this movement mathematically by saying that we will move in the direction of $-1 * functionMagnitude / gradientMagnitude$.

If both the functionMagnitude and the gradientMagnitude are positive (i.e. you are above 0 and gradient is positive), you will move in the negative direction. You can try the other circumstances with this equation and you’ll see that it always works!

$$newInput = oldInput + -gradientDirection * (functionMagnitude/gradientMagnitude) *someFactor \$$

Keep doing this, until your output for the input is “close enough” to 0.

$someFactor$ basically controls how fast you move. Like of of these “hill climbing” methods, the steps that you take are important. If you take really small steps, your computation will take longer, and if you take really big steps, you might overshoot what you’re searching for - repeatedly. The following picture should further explain why the amount we move by is $functionMagnitude / gradientMagnitude$.

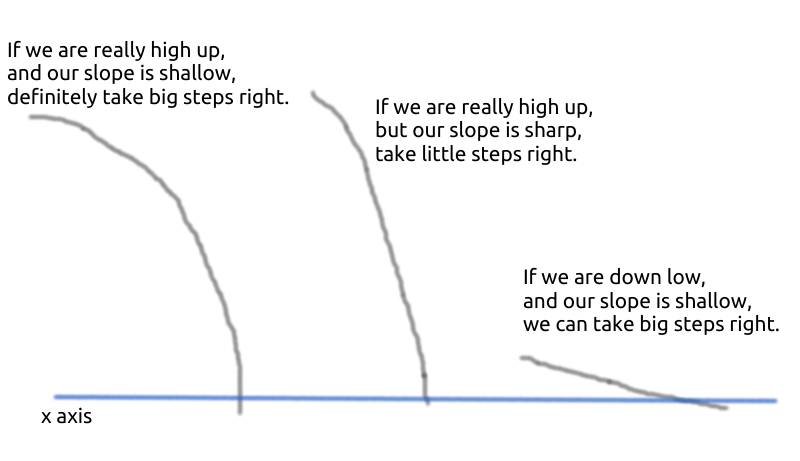
TODO redo above picture so that it doesn’t look like it was drawn by a 2 year old lol

Notice you need to be able to find the gradient of your polynomial at various points. This isn’t always possible (or practical), so let’s look at another method.

Bisection Method

Pick two arbitrary inputs, one whose output is below 0 and another whose output is above 0. Call one of your inputs “bound1” and the other “bound2”. Keep moving your bounds inwards, at all times making sure that one of them outputs below 0 and the other outputs above 0. This condition of one outputting above 0 and the other outputting above 0, let’s call that “proper”.

For example, if you try moving bound1 inwards, but notice that your bounds are no longer “proper”, then unmove bound1, and try moving bound2.

You can move your bounds a little at a time, or whenever you want to move a bound, move it in the middle of where the bound is currently, and the other bound.